• ABSTRACT
• IMPACT DATA
• VULCAN'S PERIOD VERIFICATION
• VULCAN'S ECCENTRICITY VERIFICATION
• CURRENT FORESHORTENING OF THE B SWARM'S PERIOD
• STATISTICAL CONSIDERATIONS

IMPACT DATA

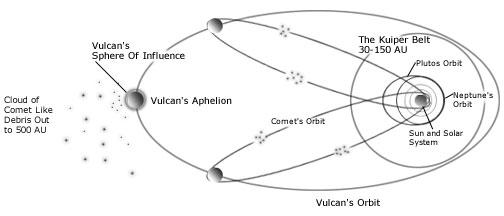
Figure 1 shows four Vulcan induced comet swarms. Two separate swarms will be generated during each successive Vulcan orbital revolution, first an A' & A then a B' & B swarm. Vulcan's eccentric orbit implies these swarm pairs will be separated by about 489 +162/-250 years. Earth impacts (see Table 1) from these swarms mark their passage near the Sun. The swarm's period is about two thirds Vulcan's.

Figure 1. Orbital Trajectories of Vulcan And Its Induced Comet Swarms.

TABLE 1 See The SYNOPSIS Section
COMET SWARM PERIOD COMPUTATIONS

*Time Of Impact (TOI) In Years Ago (YA) Measured From 2000 AD

VALUE	B':Cl-2	B':Cl-1	C:Cl-2	C:Cl- 1	A:Cl-2	A:Cl-1	A':Cl-2	A':Cl-1	B
TOI*	289	320	822	1120	1460	1765	2207	2430	3159
TOI*	3586	3628	4195	4345	4740	5195	5550	-	6370
DELTA	3297	3308	3373	3225	3280	3430	3343	-	3211
STATISTICS	Block	Total	Mean	3308	Sigma	68	Points	8
TOI*	-	7000	-	7600	-	8145	-	-	9810
DELTA	-	3372	-	3255	-	2950	-	-	3440
DELTA/2	-	3340	-	3240	-	3190	-	-	3341
STATISTICS	Block	Total	Mean	3391	Sigma	224	Points	8
TOI*	-	10300	-	-	11400	11810	12220	12640	13180
DELTA	-	3300	-	-	-	3665	-	-	3370
DELTA/2	-	3336	-	-	3330	3308	3335	-	3405
DELTA/3	-	3327	-	-	3313	3348	3338	3403	3340
STATISTICS	Block	Total	Mean	3366	Sigma	88	Points	14
TOI*	-	13650	-	14020	-	-	-	-	-
DELTA	-	3350	-	-	-	-	-	-	-
DELTA/2	-	3325	-	3210	-	-	-	-	-
DELTA/3	-	3341	-	3225	-	-	-	-	-
DELTA/4	-	3333	-	3225	-	-	-	-	-
STATISTICS	Block	Total	Mean	3287	Sigma	59	Points	7
STATISTICS	Net	Total	Mean	3317	Sigma	103	Points	37

Some of Vulcan's orbital parameters can be computed from the twenty-nine impact events listed in the SYNOPSIS section. The five-comet swarm model found in the SYNOPSIS section define which possible impact event is associated with which comet swarm (or specific comet cluster within that swarm). The Time Of Impact (TOI) is given in "Years Ago" (YA) as measured From 2000 AD. These values are listed as TOI* in Table 1.

The "Time Of Impact" (TOI) values can be used to calculate 37 separate swarm period values. The resulting time differences between impacts of comets from a given swarm (or cluster within the swarm) are divided by 1, 2, 3 or 4 depending on the anticipated number of swarm cycles contained between the impact intervals. These are listed as DELTA, DELTA/2, DELTA/3 OR DELTA/4 in Table 1. Also listed are the statistics (mean period value, sigma and number of points (DELTA or period values) used to compute the statistical values. These statistics are calculated for each major block of data for all the swarms as they extend back first one, two, three and finally four swarm cycles. Finally, the net statistical values for all the DELTA or period is computed and found to be 3317 +/-103 years based on 37 calculations.

Note that there are two comet clusters associated with four of the five comet swarms. The dual comet clusters in each swarm is likely related to celestial mechanical constraints on the formation of the 3:2 comet swarm resonate orbit, but supporting theoretical calculations have not been made. The fifth comet swarm may be part of one of the four major comet swarms deflected by a large planet or perhaps just ejected from the main swarm by out gassing. The SYNOPSIS section suggests that there may be an additional third cluster of small meteors associated with this C swarm.

Historical data indicates that either the B swarm only has one comet cluster or that the two comet clusters contained within the swarm must be very close together. The first table in the SYNOPSIS section suggests that the predicted return of the B swarm will occur in the 2006 to 2012 time frame. The first may arrive (or coming into view) 2006 or early 2007 and the latter passing around 2010 - 12 (or as late as 2016). Thus, these predictions are consistent with the B swarm's clusters being close together.

Up to four cycles of nine specific comet clusters are identified, but only four have significant data to illustrate possible period variation.

• A:Cl-1 1 swarm (6 Period Measurements ) - 3315 +/- 208 years
• B':Cl-1 swarm (10 Period Measurements ) - 3333 +/- 19 years
• C:Cl-1 swarm (6 Period Measurements ) - 3230 +/- 14 years
• B: (6 Period Measurements ) - 3351 +/- 72 years
• Mean Period Measurements 3317 +/- 104 years

VULCAN'S PERIOD VERIFICATION

The geological climatological impact offers hard physical evidence that Vulcan actually exists. The first table in the SYNOPSIS illustrates probable impact dates. Note that B'(10,300 YA) - B'(320 - 289 YA) represents three comet swarm B' periods and equals about 10,000 years. Vulcan's New Orbital Parameters estimates Vulcan's period to be 4,969 years (with a comet swarm period 3,313 years). Likewise 10,000 years is about two Vulcan orbital periods. This reflects the (3:2) comet swarm to Vulcan orbit resonance. Fitting the impact data in the Synopsis section to Vulcan orbital theoretical period (4,969 years) implies a +/- 105 year sigma uncertainty [3/2 X (3,313 +/- 70 years)].

The mean +/- sigma uncertainty for all 37 swarm periods listed in Table 1 is 3317 years (verses a 3313 predicted period) +/- 104 years respectively. Vulcan's period and sigma uncertainty should be 3/2 times greater or 4975 years +/- 156 years respectfully. Thus, the mean value and sigma error in the derivation of Vulcan's orbit period by computing individual comet swarm periods is about the same as fitting the comet impact data to a 4969 year (3313 year comet swarm) period.

Vulcan's orbital period is both theoretically computed and calculated directly in two ways from the comet impact data. Forbes was the first to discover a possible planet in the outer solar system with a nominal 5000-year period more than a hundred years ago. See Table 2. But his data was "thin". The comet impact data "fits well" as it leads to verification of the theoretical orbit period. The error residuals computed by all the methods overlap.

TABLE 2
VULCAN ORBITAL PERIOD COMPARISONS

a. IRAS Data, Partial Tzu Wei Chinese astrological, Esoteric astrology.*
b. Cambridge Conference Archives Of Possible Impact Events.
c. IRAS Full Tzu Wei Chinese astrological, Esoteric astrology, 2 Sigma Error.*
d. No IRAS Full Tzu Wei Chinese astrological, Esoteric astrology.*
*See: 'ASTROLOGY AS SCIENTIFIC AS ANY OTHER STREAM OF SCIENCE' or STARS AREN'T SMILING DOWN ON 2002 - Much depends -- according to Sergei Bezborodny, head of the astrology center at the Central House of the Russian Army. - Moscow Times January 11, 2002 - JOHNSON'S RUSSIAN LIST - By Kevin O'Flynn Staff Writer

Computed Orbital Period	Error Range	Technique Employed
THEORETICAL	VULCAN	ORBITIAL PERIOD
5,030 Years (1997 Paper)	+/- 125 Years	IRAS/Astrological Techniquea
4,969 Years (2002 Paper)	+/- 12 Years	IRAS/Astrological Techniquec
4,972 Years (2002 Paper)	+/- 27 Years	No IRAS/Astrological Techniqued
COMPUTED	VULCAN	ORBITIAL PERIOD
5,000 Years (1878)	+/- 200 Years	Forbes Comet Aphelia
4,969 Years (2003 Synopsis)	+/- 105 (or 137) Years	Fit To Comet Impact "Lore" Datesb
4,975 Years (2003 Synopsis)	+/- 156 Years	Swarm Return/Comet Impact Lore

It is important to notice that a Russian Army Astrology Center exists. Astrology is a tool used by Heads of State (e.g. Ronald Reagan) and both military and diplomatic corps around the world. It will be shown in the STATISTICAL CONSIDERATIONS Section, using measured error residuals from the comet impact data, which set of orbit parameters best represents Vulcan's orbit, the C"EV or C*EV orbit.

VULCAN'S ECCENTRICITY VERIFICATION

A planet's Sphere Of Influence (SOI) is the region around it that it can practically hold an object like a satellite. Theoretically, this should be an infinite distance, but nearby objects limit the range. Vulcan's SOI was scaled to that of Pluto because they are both distant objects of nominally the same density. Pluto's SOI has been computed by Van Flandern to be 10⁷ kilometers. Scaling this to Vulcan yields:

Vulcan's SOI = (Pluto's SOI) X (Vulcan's Maximum Distance)/(Pluto's Minimum Distance) X (Vulcan's Diameter)/(Pluto's Diameter)

51.3 AU = 10⁷ km X (444.44 AU/29.64 AU) X [330/(1/400)]^1/3

51.3 AU of Vulcan orbital motion at this point corresponds to 259 years. The errors in Pluto's SOI and mass are assumed to be about 10%. The error in Vulcan's mass is unknown, but assumed to be 30%. Thus, the relative error in Vulcan's SOI is:

RE _{Vulcan's SOI} = 0.1 + 1/3 X (0.1 + 0.3) = 0.233

This corresponds to 60 years of motion. Thus, the net possible heliocentric longitudinal separation of Vulcan and the comet swarm at the A' and A or B' and B points, is +/- 319 years. But if the comets get within a range where Vulcan's gravity equals or exceeds that of the Sun (as quantified by the mass angle ratio), they could be gravitationally ejected from the solar system. This range corresponds to about 1.8^o or +/- 70-years.

There seems to be a fundamental difference between clusters of the B' and B swarms verses the A' and A swarms. The large separation of the A' and A clusters may be due to their orbit being nominally in Vulcan's orbital plane. Thus, the motion of Vulcan must be factored in to the resulting larger separations observed. Alternately, the B' and B clusters may be in an orbit nominally perpendicular to Vulcan's orbital plane. Thus, these comets move rapidly by while Vulcan is relatively stationary. The separation of the B swarm's clusters is so small that it is hard to measure, perhaps only a few years. Thus, the B' -> B clusters offer a better measure of Vulcan's eccentricity. The actual 515 year value may have to be modified by the 330 or 370 year intra-swarm cluster separation to generate the observed A' to A cluster separation (of about 774 years). Indeed, two times [191 years minus 70 years]) does equal a 242 year range that would occur when the comet swarm would be within Vulcan's sphere of influence but not so close to be captured or ejected by it. This value, when added to the 515 year value is around 757 years, or close to the 774 year value observed.

CURRENT FORESHORTENING OF THE B SWARM'S PERIOD

The real question is when should we anticipate the next major comet swarm to passby and threaten Earth?. The following figure, taken from Tollmans' work, shows what it was like 9,800 years ago.

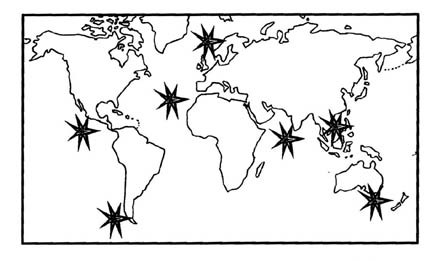
Figure 2. Earth Impacts 9800 Years Ago Due To The Passage Of Comet Swarm B.

Then, the B-swarm strike of 7810 BC (or 7640 BC) appears to have been a multiple event as depicted above. It caused a world wide catastrophe. This occurred while Vulcan was near aphelion as it is now. The inner planets are now at a maximum distance from the barycenter of the Sun/Vulcan system as they were then. When the inner planets are farthest removed from the barycenter, they could be in a position that would expose them to a maximum risk of impacts from the B-swarm's comets. Long period comets do not always just "skim by" the Sun. Some actually collide with the Sun while others can miss by almost the distance of the Sun to the Earth.

As time passes, the comets within their respective swarms tend to spread along their orbital trajectories due to gravitational interaction with the Sun and its planets. Thus, impact intervals (detected on Earth via weather changes) broaden. Still, the A ->A' and B ->B' impact intervals appear to be easily isolated and identified. Swarm C is suspected of being deflected by gravitational interactions and recent impacts from it (1,000 YA) may also have spread. Swarms B and B' seem to have spread the least, only an average of 37 years for Swarm B' and an undetectably small amount for Swarm B.

The B-swarm would be expected to pass about 2154 AD assuming a base point of 3159 years ago (the Bronze Age Collapse) and that an average swarm period of (3313 years) can be added to it. But each swarm is different and other factors may have an influence on their trajectories modifying of their orbital periods. Table 3 offers a compiled list of all Swarm B period measurements.

TABLE 3
FORESHORTENING OF THE B SWARM'S PERIOD

Date	Period	Delta Period
13180 YA	-	-
9810 YA	3370	-
6370 YA	3440	-70
3159 YA	3211	229
2012 AD??	3171?	40?

Notice the shortening of the last measured B comet swarm period. The last observed period measurement was 3211 years and when this is added on to the 3159 year ago impact date, the next predicted passage should occur circa 2052. The rms error of the B-swarm is 72 years.

The 1908 Tunguska strike could be one of the first impacts from this (B) swarm. However, the bulk of the main cluster has been predicted to pass through the inner solar system in the 2006 to 2016 time period. This would amount to a further 40-year fore-shortening of the B comet swarm's orbital period.

The oscillations of Sol and our solar system in the galactic plane may have an influence on the trajectories of the threatening comet swarms. Our solar system bobs up and down in the galactic plane as it orbits the galactic center every 180 to 250 million years. A reversal of direction of motion occurs when our solar system passes through the peak of this oscillation. The period of the bob or oscillation appears to be around 4 million years. Sol languishes near this peak for a relatively long period of time, hundreds of thousands of years. This is where we are now.

The above oscillation of Sol can modify one of the comet swarm's impact periods if Sol is near the peak. Normally, the 2006 - 2016 AD impact prediction should be viable since the B swarm has been orbiting in "free" space unperturbed by either Vulcan or the Sun (a pass near Vulcan could perturb the comet swarm's orbits, but this happens only every 10,000 years). As Sol rises, the part of cometary orbits ahead of Sol's upward movement will be attracted very gradually downward. But at the point of turn-around and there after, their orbits will begin to stretch again. The reverse is true of comets that are in that part of their orbits between our Sun and the galactic plane.

Astronomical calculations (private communication) made in the 1980's suggested that Sol has is approaching the top of its oscillatory cycle 24.5 light years above the galactic plane. Speeds during this phase are very much lower than when near the galactic plane, ~1 kps compared to 50 kps. 3,000 - 3,300 years is estimated to complete the reversal. Note that this is about the comet swarm's estimated period (3313 years). Of course, Sol's exact location in this cycle is difficult to measure precisely. However, we could now be near its apex.

As the Sun, or any of its orbiting bodies, departs the apex of the galactic oscillation, the velocities change at a slightly different rate. Assuming the velocity rising vertical to the galactic plane is given by:

v = 50 kps sin wt

where w = pi/(2 X 1 0⁶ years)

Then dv/dt = 50 w cos wt.

The velocity differential for comets 1600 years ahead of the Sun would be

dv = (50 X pi X 1600)/(2 X 10⁶) = 0.13 kps

The nominal apex for comet swarm A (& B) and A' (& B') are at 444.4 AU, RA's 276^o and 251^o, and dec.s are 25.4 ^o and 22.5^o respectively. Swarm A (& B) and A' (& B') declinations to the galactic plane are 16.7 ^o (& 37.1^o) respectively.

Usually, when both the Sun and comets are rising upward or downward from the galactic plane, the same galactic plane gravitational force acts on both. But when just turning downwards, the reversal of directions will not be precisely balanced. Instead, it will appear to modify the comet's apparent velocity. Assume that half the comets period (1600 years) is spent moving downwards while Sol is moving upwards. The vertical velocity due to the galactic oscillation near its apex is moving at about 0.13 kps. The modification to the comet swarm's relative velocity would be an increase of about [0.13 kps X sin (declination)] or 0.038kps. This amounts to a 2.9% increase of the swarm's mean velocity of about 1.32 kps. Thus, it could shortened the apparent half swarm period by about [0.029 X 1600/(1 + 0.029)]. It is assumed that the first half of the comet swarm period is not affected because both the comets and Sol are going in the same (upward or downward) direction. Consequently, the foreshortening of the observed B swarm period near the apex of our oscillation in the galactic plane would be about 45 years. This may account for the 40 year miss-match between the predicted 2006 - 2012 and projected 2052 impact dates. Still, it is very difficult to accurately model how the galactic forces influence the date of the next B swarm's pass.

The actual comet "lore" impact data supports this contention. See Table 3. Note that the interval of the B swarm impacts from 13180 YA to 3159 YA first lengthens, then shortens relative to the theoretical 3313 year value.

STATISTICAL CONSIDERATIONS

The reported times when Earth's atmosphere has been determined to be dusty or cold are largely extracted from the Greenland Ice Core sample data (during the Younger Dryas geological period) or from tree ring data found in specimens covering the last 6000 years. These conditions may be caused by comet impacts of various sizes. A hypothesis is offered whereby these patterned occurrences are related to five Vulcan induced comet swarms passing through the inner solar system. An array of 37 separate computations of these (similar) periods has been culled from this data with a mean period of 3317 +/- 104 years. Further, it is hypothesized that these comet swarms are formed in a 3:2 orbit resonance with Vulcan's orbit. Thus the mean comet swarm period (when multiplied by 3/2) offers an independent estimate of Vulcan's period (4975 years +/- 156 years). The statistical P-value of the Student's t-test was computed using both theoretical Vulcan periods for the favored C"EV orbit and the comet impact derived period and related uncertainty. The P-value was found to be >0.4 for the first (IRAS point - 4969 year period) case and >0.23 for the second (no IRAS point - 4972.1 year period) case. Statistics cannot be used to support a hypothesis, but they can be used to refute one.* Since the computed P-values are well above 0.05 in both cases, statistically a significant difference between the two ways (theoretical and impact data) to compute Vulcan's period cannot be detected. Thus, there is no statistical evidence to reject the proposed hypothesis that the theoretical Vulcan period of 4969 years is associated with comet impact events. By contrast comparing the high end values for the period of the other proposed Vulcan C*EV orbit (5058.7 years) both the IRAS (5070.2 years) and no IRAS (5089.1 years) periods yielded a highly significant (p-value <0.001) indicating rejection of the hypothesis of equality. Thus, statistically, the longer period C*EV Vulcan orbit appears to be rejected by the impact data.